Grafy nad Odrą

- Tato, kiedy mi wreszcie powiesz jak rozwiązać zagadkę z mostami w Królewcu? – zapytał Bit z pretensją w głosie.

- Nie teraz, idź z kolegami zagrać w piłkę. – odpowiedział automatycznie Tata wpatrzony w ekran komputera,

- Ale Tato, na dworze jest –20 stopni Celsjusza, środek zimy, wszędzie zaspy, nie da się grać w piłkę!

- To idź z siostrą poukładaj puzzle, gdzieś jeszcze jest ta układanka na 20 tysięcy kawałków...

- Ale Tato, Beta wczoraj ułożyła te puzzle na podłodze, zostawiłeś otwarte drzwi i sporo puzzli zjadł nasz pies Epsilon!

Do Taty dotarło, że się nie wymiga tak łatwo. Odłożył komputer, spojrzał na syna. ,,Ale on szybko rośnie’’ pomyślał a na głos powiedział.

- To chodź do kuchni, tam mamy tablicę, przyda nam się.

Królewiec, dzisiaj Kalingrad, znany jest z wielu rzeczy, ale być może najbardziej ze sławnego problemu z mostami.

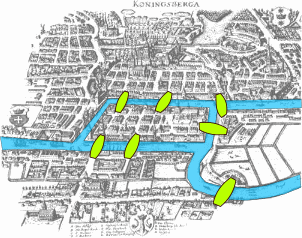
Mamy rzekę, która opływa z dwóch stron wyspę, tak jak na rysunku po prawej.

Przez rzekę jest przerzuconych 7 mostów tak jak na rysunku.

To znaczy tak było kiedyś, dzisiaj tych mostów jest mniej, ale w czasach Eulera było ich 7 i to lepsza liczba dla zagadki.

Zagadka:

Czy da się znaleźć taką drogę spacerową aby przejść przez wszystkie 7 narysowanych mostów w Królewcu ale przez każdy tylko raz.

- Tato, ja znam treść zagadki, tylko nie znam rozwiązania! – Zniecierpliwił się Bit.

- Nie da się. – odpowiedział Tata.

Zapadła niezręczna cisza.

- To jest rozwiązanie. Nie da się znaleźć takiej drogi! – Rozwinął swoją wypowiedź Tata.

Zastanawiasz się teraz drogi czytelniku, czemu Tata jest tak nieuprzejmy w stosunku do swojego kochanego dziecka? Nie dość, że odpowiada półsłówkami, nie wyjaśnia problemu to jeszcze tylko podaje suchą odpowiedź?

No cóż, mnie to też zastanawia. Nie popieram takiej postawy. Dlatego teraz ja, narrator, opowiem Bitowi na jego jakże ciekawe pytanie.

Nad problemem mostów w Królewcu głowił się w XVIII wieku Leonhard Euler, wybitny szwajcarski matematyk, twórca wielu nowych gałęzi matematyki.

Zapytasz się jak się tworzy nowe gałęzie matematyki?

W tym przypadku Euler rozwiązał zagadkę z mostami w Królewcu. Ale to mu nie wystarczyło, zaczął się zastanawiać ile musi być mostów i wysp aby dało się je zwiedzić zgodnie z regułami zagadki a kiedy nie da się znaleźć odpowiedniej drogi.

Zamienił więc jeden problem na wiele podobnych problemów.

A następnie wymyślił nowy sposób patrzenia na te problemy by znaleźć jedno rozwiązanie dla nich wszystkich. To był początek działu matematyki, który dzisiaj nazywamy teorią grafów.

Ale po kolei, jak rozwiązać tę zagadkę? Pierwsze co zauważył Euler, to że dla zagadnie nie ma znaczenia jak duża jest wyspa czy jak duże jest wybrzeże, liczy się tylko z jakiego obszaru można dojść do którego obszaru. Oznaczmy obszary literami A, B, C i D a mosty literami a, b, c, d, e, f i g.

Zastanawiasz się może teraz dlaczego nazywać wyspę ‘A’ a nie ‘wyspą pośrodku Królewca’? Chodzi o zwięzłość zapisu. Zamiast opisywać drogę ‘Przejdź z wyspy po środku Królewca na południowy brzeg przez pierwszy most po lewej’ możesz krócej powiedzieć ‘Przejdź z A do B przez a’.

Krócej.

A krócej to często lepiej!

Drugie co zauważył Euler to, że sama rzeka nie ma znaczenia. Liczą się tylko połączenia, który obszar łączy się z którym obszarem i iloma przejściami. Gdyby wymazać zbędną rzekę to zostanie taki rysunek.

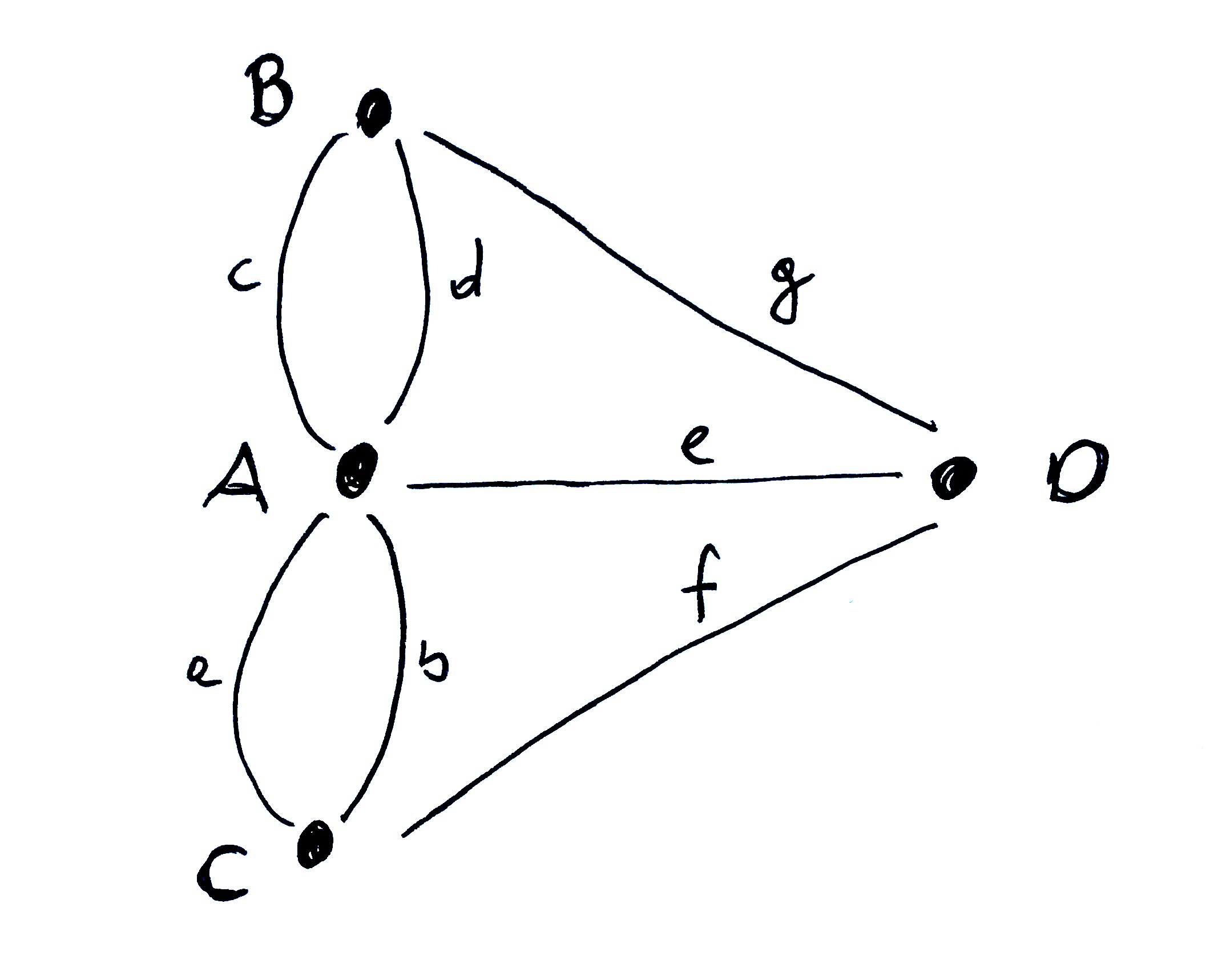
Takie rysunki nazywają się grafami. Mają węzły (A, B, C i D) oraz krawędzie łączące węzły (a, b, c, d, e, f, g).

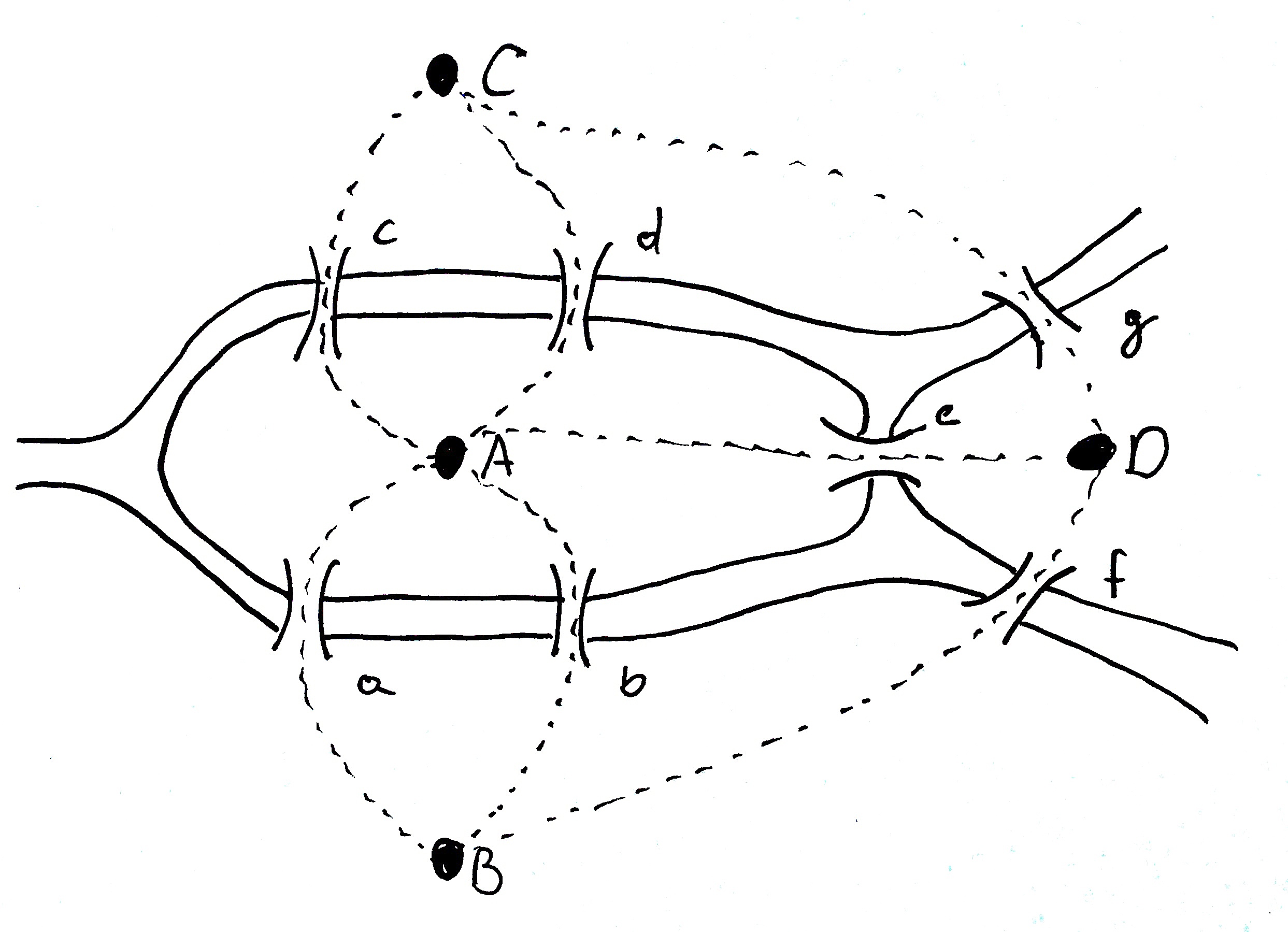
Taki graf opisuje wszystko co ważne w zagadce i usuwa wszystko co zbędne. Łatwiej myśleć o problemie gdy się pozbędzie zbędnych rozpraszaczy. Usunięcie zbędnych informacji to ważna umiejętność matematyków. Euler był w tym bardzo dobry.

Ostatnia rzecz, którą musimy wiedzieć aby rozwiązać zagadkę z mostami, to musimy umieć policzyć ile jest wyjść z każdego wierzchołka (czyli mostów z każdego obszaru).

To możemy policzyć razem.

Z wierzchołka A jest 5 wyjść. Z wierzchołka B, C i D są tylko po 3 wyjścia.

Euler udowodnił takie stwierdzenia: (dla grafu spójnego, ale nie przejmujmy się w tej chwili tym co to znaczy):

- Jeżeli każdy wierzchołek ma parzystą liczbę wyjść to ZAWSZE da się znaleźć drogę zgodną z regułami zadania.

- Jeżeli tylko 2 wierzchołki mają nieparzystą liczbę wyjść to ZAWSZE da się znaleźć drogę zgodną z regułami zadania, co więcej ta droga zacznie się w jednym z nieparzystych wierzchołków a zakończy w drugim.

- Jeżeli więcej niż 2 wierzchołki mają nieparzystą liczbę wyjść to NIGDY nie da się znaleźć drogi zgodnej z regułami zagadki.

Niesamowite, prawda?

U nas wszystkie 4 wierzchołki mają nieparzystą liczbę wyjść więc nie da się znaleźć dobrej drogi.

Ale pewnie jesteś ciekaw DLACZEGO tak jest?

Spójrz jeszcze raz na ostatni rysunek. Zauważ, że gdybyś przechodził po tym grafie zmazując krawędzie, to za każdym razem wchodząc i wychodząc np. do obszaru A zmażesz jedną krawędź wchodzącą i jedną wychodzącą. Więc każde przejście przez obszar usuwa z grafu dwie krawędzie dla tego wierzchołka.

Chcesz przejść wszystkie mosty, czyli chcesz usunąć wszystkie krawędzie.

Ale jeżeli nieparzystych wierzchołków jest więcej niż 2 to tego się nie da zrobić. Ponieważ w pewnej chwili każdą nieparzystą liczbę zredukujesz do 1 i będziesz w sytuacji bez wyjścia. Będziesz mógł wejść na jeden z czterech obszarów, ale już z niego nie będziesz mógł wyjść -- zabranie drogi wyjścia.

To przewrotne wnioskowanie. Zastanów się nad nim i gdyś potrzebował dalszej pomocy – daj znać!

Sprawdź się!

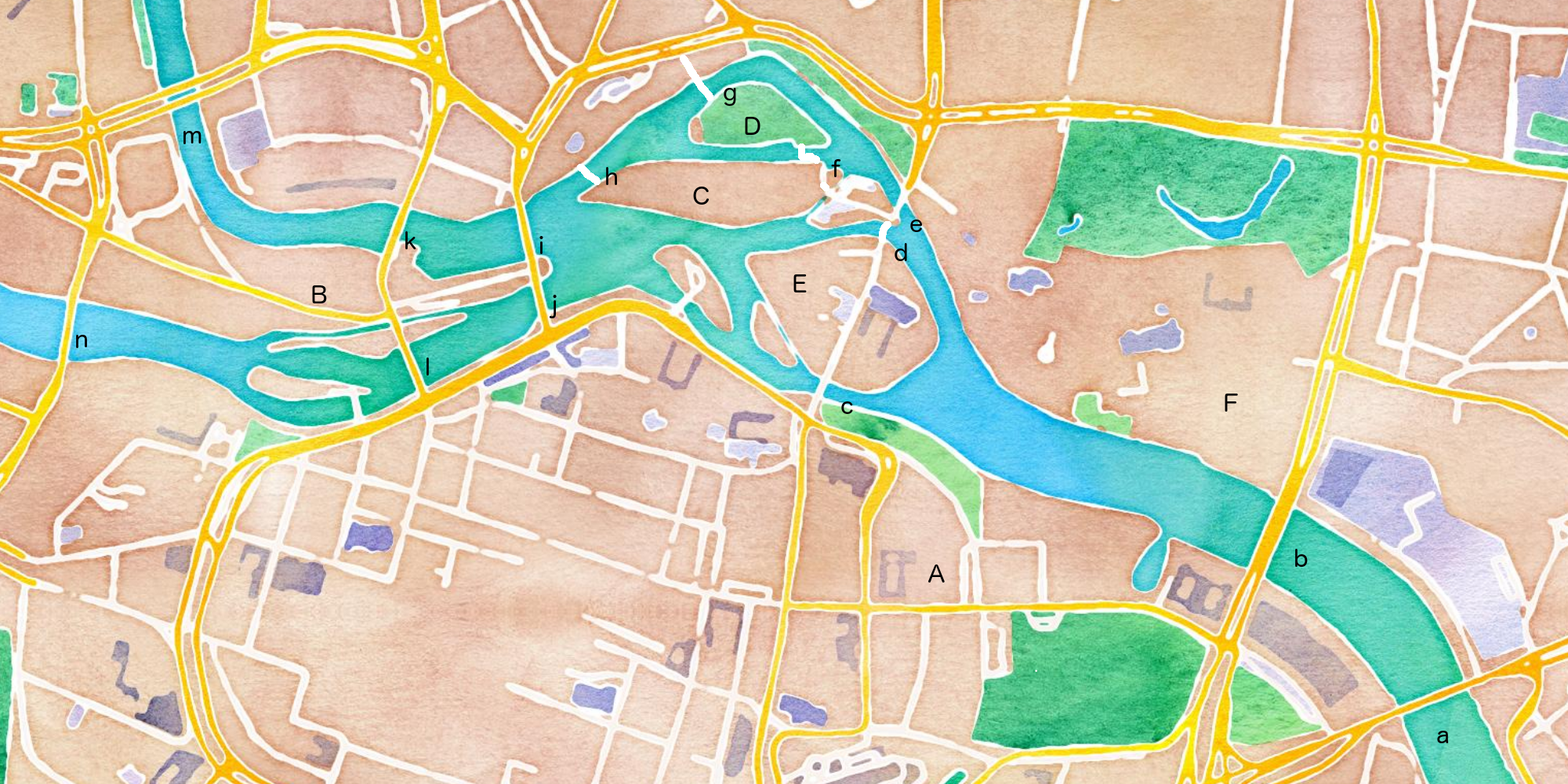
Euler rozwiązywał problem dla 7 mostów. Czy poradzisz sobie czytelniku z 14 mostami?

Poniżej jest mapa centrum Wrocławia, miasta nad Odrą.

Narysuj dla niego graf a następnie sprawdź czy da się przejść przez wszystkie mosty przechodząc przez każdy tylko raz.

Mosty: a) Most Grunwaldzki, b) Most Pokoju, c) Most Piaskowy, d) i e) Most młyński, f) Most Św. Klary, g) Kładka Żabia, h) Kładka Śłodowa, i) i j) Most Uniwersytecki, k) i l) Most Pomorski, m) Most Mieszczański, n) Most Sikorskiego

Obszary: A) Rynek, B) Kępa Mieszczańska, C) Wyspa Słodowa, D) Wyspa Bielarska, E) Wyspa Piasek, F) Katedra